|
E.M.G. Woes: Toward A More Consistent Normalization
| |||||||||||||||||||||||||||||||||||||||||||||
| MWC and EMG lost by taking Position 1: |
Case A: 3-away, 2-away Doubled to 2 |
Case B: 3-away, 3-away Doubled to 4 |
Case C: 3-away, 5-away Doubled to 8 |
|||||
|---|---|---|---|---|---|---|---|---|
| Snowie 4.5 | ||||||||
| gnubg 0.14 | ||||||||
Both Snowie and gnubg "understand" that the three decisions are identical. Snowie thinks each take sacrifices 5.26% MWC while gnubg thinks each take loses 5.1%, and these are the numbers they use to make match play decisions. However, they each report three substantially different EMG errors for the bad takes at the different scores. Snowie reports that Case A is a .425 quadruple whopper, Case B is a .212 double whopper, and Case C is a .141 single whopper, while gnubg (using the g11 match equity table) shows the same pattern: .407, .203, and .136.
Does this make any sense? In what way can choosing the lesser of the same two options, giving up the same MWC, be three times worse in one case than another?
2. Measuring equity in money and match-play.
Let's take a closer look at what the EMG calculation does:
The proper unit of measurement in money backgammon is the point. All games end with a gain or loss of 1, 2, or 3 points, multiplied by the value of the doubling cube. A position is worth some fraction of points, and a checker-play or cube error sacrifices some fraction of points. A last-roll position with 20% game-winning chances has an expectation of .2 -.8 = -.6 points per game. Accepting a cube in that position is an error because the doubled equity of -1.2 is two-tenths of a point worse than passing and losing a single point. The size of the error is .2 points.
A backgammon match has only two end-states: a win or a loss. The proper unit of measurement is the probability of winning the match, or Match-Winning-Chances (MWC). MWC start at 50% (assuming equal players) and drift up and down, ultimately reaching 0% or 100%. Checker-play and cube errors sacrifice MWC. Accepting a cube for the match with 20% game-winning-chances when the alternative is passing and trailing 3-away, 1-away (with MWC of 25%) sacrifices 5% MWC. Programs like gnubg and Snowie make match-play decisions by calculating the expected MWC of legal alternatives and selecting the alternative with the highest expectation.
However, using the metric of MWC to discuss match-play errors has a often-unwanted property: Errors made at the beginning of a long match have less of an impact on the outcome than errors made at the end. A checker-play blunder giving up 10% game-winning chances at the beginning of a 17 point match loses less than 1% MWC, but the same play at DMP gives up 10% MWC. The magnitude of an error's lost MWC tells us more about when the error occurs within the match than about the quality of the error in the abstract.
Enter the Equivalent to Money Game (EMG) transformation, first introduced by Roy Friedman in the article "Tailoring Cube Action To The Match Score," in the February 1991 issue of his magazine Leading Edge Backgammon. Friedman writes:
To circumvent the drawbacks of raw match equity, I use a measurement called Normalized Expectation. Normalized Expectation is simply the raw match equity of a position scaled to the interval -1.0 to +1.0 where -1.0 represents the match equity when the opponent cashes the current game and +1.0 represents the match equity when you cash the current game. In this way, the guideposts from money backgammon remain applicable, regardless of the match score. For example, if your Normalized Expectation is +1.1, your opponent has a close pass; if your Normalized Expectation is +.9, your opponent has a close take and you probably have a strong double.It is of historical interest that Friedman introduced the concept just before the modern era of computer-assisted backgammon analysis. (In fact, a review of Expert Backgammon, the last important commercial backgammon program not based on neural-net architecture, appears in the same issue.) Re-reading the article sixteen years later highlights just how far backgammon theory and practice has progressed. Specifically, Friedman's goal was not to provide a better way to measure the size of errors from recorded matches. To do that, one would first need the MWC value inputs to produce EMG value outputs, and where would those MWC values come from? Snowie, the first tool publicly available to analyze backgammon matches rather than positions, wouldn't come into existence for another seven years after Friedman's article.
Instead, Friedman's goal was to better understand the properties of specific match scores. He took four reference positions (a race, a blitz, a prime v. prime, and a crunch), reported their money-play equities (usually generated by manual rollouts) and also their calculated EMG values for a range of scores. For instance, a race which is a bare money-take (eq. = .95) turns out to be a weak No-Double when 5-away is on roll against 2-away, 3-away, or 4-away (EMG values of .6, .65, and .65). From this Friedman concludes:
When you are five points from victory, you should be reluctant to double in positions with little or no gammon threat. For the reasons described above, there's a relatively high utility in collecting one point to get to a score four points from victory. Assuming your opponent knows this, he will not readily cede such an important point by passing. Your opponent's inclination to take a non-gammonish double implies that you can delay such a double until you have a considerably larger advantage than you need to double in a money game. On the other hand, in positions with a moderate or strong gammon threat, you can double fairly normally at a score five points from victory because winning a gammon has the benefit of reaching the Crawford game.This is the kind of information that EMG was originally designed to produce: general properties of match-scores and their systematic differences from money play. In fact, I still remember the exact phrasing of some of the article's "helpful generalizations" which influence my match-play decisions to this day. What I didn't remember was that this article introduced the EMG calculation in the first place.
Of course, students don't really use EMG values in this way anymore. Now we set our bot de jour to highlight all our match-play EMG errors greater than .1, or .05, or, if we're feeling particularly masochistic, .03. "Rats, I'm still making .2 errors in holding games," we say, confident that the category of .2 errors is meaningful and stable. Then we average all our EMG errors over a match (briefly debating whether to divide by the number of unforced moves or total moves) and calculate our Error Rate. Sometimes we even bet on Error Rates rather than the outcome of the match.
Eventually history repeats itself, and someone else discovers that comparing EMG values might be a good way to think about cube-actions at various match scores. In a 2003 column for GammonVillage titled "Match Play Vs. Money Play," Douglas Zare writes:
The following table indicates how much it is worth if your opponent accepts a 2-cube that would be a borderline money take, expressed in terms of EMG on a 1-cube. These are Snowie's evaluations of a long race with 21.5% winning chances.
These are precisely the data that Friedman reported in 1991: the EMG values of a borderline money-take race across different scores. Again, note the low values when 5-away is on roll against 2-away, 3-away or 4-away (.808, .861, .860). These differ from Friedman's .6, .65, and .65 because they are based on different match equity tables, but their lesson is still the same: double later in races when trailing 5-away. Zare also provides a table for recubes to 4, which Friedman did not:
Zare notes that the 25.2% racing take-point for a recube to 4 at 3-away 3-away is "conveniently close to the 25.3% racing take point on an initial double [at that score]," and sees that the EMG error value at 3-away 3-away (cube to 2) is much larger than the 3-away 3-away (cube to 4): "Of course [one] error looks much smaller than [the other], but the same conceptual error may be at the heart of both; only the normalization is different." Perhaps Zare would have been more intrigued had he compared the 2-away 3-away cube to 2 (.301 by his table) to the 3-away 3-away cube to 4 (.151). There the take-points aren't merely close but are identical, because the decisions themselves are identical.
Zare goes on to provide similar tables for a blitz position, effectively duplicating the structure of Friedman's article, twelve years later. I'm not chiding Zare—far from it. He wrote a great piece on a great topic. Besides, I did something similar three years after that. In 2006, I wrote a program that automates the process of asking gnubg for its opinion about a particular cube decision across a range of match-scores. Here is its output for Position 1:
Cubeless and cubeful money-play equities are presented to the right of the diagram: Black has an 80.2% CPW, for a cubeless equity of .604. For money, he is right to double by .110 (not doubling would be a .110 error), and White's take would be a .087 error.
EMG values for various scores are presented below. The top line indicates that when tied at 7-away, Black should give an initial double and White should pass. Not doubling would be a .106 error, and taking would be a .110 error. I hoped that examining this kind of data for different positions would help illustrate the properties of specific match-scores. (What a novel idea. Hey look—most every score in the table is a pass, but 5-away doubling 4-away, 3-away, and 2-away are all takes!) I learned a lot from the program, but am embarrassed to report that it took me over a year to realize that the -.407 value when 2-away doubles 3-away to 2 should be the same as the -.203 value when 3-away doubles 3-away to 4. In fact, that was the specific observation that lead to this investigation and this paper. Which brings us back to our main topic.
So is this really a problem? Is the take of an initial double at 3-away 2-away really the same as the take of a redouble at 3-away 3-away? After all, the score sheets look different. I'm happy to argue that they are, indeed, the same in every important respect. A backgammon position is not really what's on the board—it is all the legal continuations from what's on the board. Two positions may look different, but if they present the exact same set of options, they are the same position. In this regard, the take of an initial double at 3-away 2-away really is the same as the take of a redouble at 3-away 3-away, or the take of an 8-cube at 3-away 5-away. Similarly, the take of an initial double at 4-away 2-away really is the same as the take of a redouble at 4-away 3-away, or the take of an 8-cube at 4-away 5-away. Any rating system that treats these cases as different is not reflecting how backgammon really works.
3. Looking at the problem.
A good way to understand what the EMG transformation does is to consider it visually: We plot Match Winning Chances (the starting inputs of the process) on the horizontal x-axis, and EMG points-per-game (the result of the transformation) on the vertical y-axis. (All diagrams in this paper will be from Black's perspective, and employ his MWC rather that White's, regardless of who is on roll.)
Let's examine the 3-away 2-away case, and graphically represent gnubg's calculation of a .407 error. If 3-away takes with only 19.822% Game Winning Chances he is making a mistake, costing himself 5.1% MWC. But how much is that error on the EMG scale? To find out, we plot the two points associated with +1 and -1 at this score. If 3-away were to win one point he would be tied at 2-away, 2-away, with 50% MWC. We plot the point .5 MWC against 1.0 EMG. If 3-away loses one point, he will trail 3-away, 1-away for 24.923% MWC, so we plot the point .24923 MWC against -1 EMG. These two points form the line which determines the EMG associated with any other point on the MWC x-axis.
If 3-away takes the 2-cube, he will play for the match with 19.822% Game-Winning and Match-Winning Chances. To find the EMG for 19.822% MWC we extend the blue line down and to the left until it crosses the x-axis value of .19822. It does so at the blue data-point, with an EMG value of -1.407. Taking is a .407 error, since passing has an EMG value of -1.0.
What's happening at the 3-away 3-away and 3-away 5-away scores to produce EMG error values of .203 and .136?
Here we see the EMG lines of all three cases. Each line passes through the same point: 24.9% MWC on the x-axis plotted against -1 EMG on the y-axis. This reflects that in all three cases, passing the offered cube produces the score 3-away 1-away (Crawford), resulting in 24.9 MWC. It is the anchor point at +1 EMG, reflecting what happens when 3-away cashes rather than gets doubled, which accounts for the difference between the lines. In case A, when 3-away wins one point, he reaches 2-away 2-away, for 50% MWC. In case B, when 3-away wins two points, he reaches 1-away 3-away (Crawford) for 75.1% MWC. And in case C, when 3-away wins four points, he wins the match. Those three values (50%, 75.1%, 100%) determine the slope of each EMG line, which in turn determines the three different EMG values for 19.8%: -1.407 in case A, -1.203 in case B, and -1.136 in case C.
This means that 3-away's cash point is influencing the EMG value of his take, which is odd since his cash-point has no relevance to his take-pass decision. In fact, once 3-away is doubled, it is no longer possible for him to win the un-doubled cube value. Yet that impossible outcome determines the EMG-value of his take.
4. Toward A New Normalized Expectation.
I would love to propose a New Normalized Expectation (NNE) which has all the useful properties of EMG, yet avoids the inconsistencies described above. As of this draft, I don't have one. Here are my thoughts and efforts so far. (This section in particular owes a great debt to David Montgomery, who provided much help in model-building.)
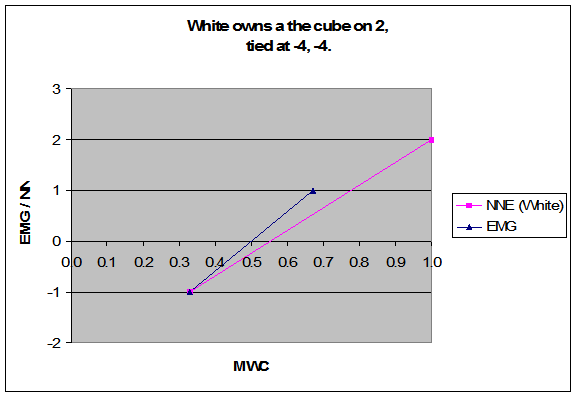
A natural place to start is a normalization scaled to the interval +1.0 to -2.0, where 1.0 still represents the MWC of winning the game at the current cube value, but where -2.0 represents the MWC of losing the game at the subsequent cube level. This interval does indeed eliminate the inconsistencies described above because it focuses on what is common to cases A, B, and C: The MWC of passing or losing the current game (24.9%), and the MWC of winning the game at the next cube level (100%).
The diagram below shows the same three EMG lines for the scores we have been discussing, plus the additional NNE line that is common to all.
In this case, that NNE line is almost (but not exactly) identical to the yellow EMG line reflecting the score of -3, -3 (doubled to 4). Accordingly, the NNE error of .2038 is almost (but not exactly) identical to the EMG error of .20341. This similarity is in some part coincidental (due to the exact values of the g11 match equity table), and does not persist at other scores.
For example, the next diagram shows the same results for the scores -4,-2; -4, -3; -4, -5. This is the same sequence of scores that we have been discussing all along, except that the player being doubled is 4-away rather than 3-away. In each case, that player can pass and end up trailing -4 -1 (Crawford) for 18.23% MWC, or can take and play for the match. Let's give our player 15% MWC, which means that the take is an error that sacrifices 3.23 MWC. Again, Snowie and gnubg understand that all three takes give up the same MWC, and again they each give different EMG errors to three takes (.292, .155, and .079.) The single NNE line is different from each EMG line, and provides an error value of .119.
To this extent, NNE does what is asked of it: it evaluates the take decisions in each set of three example cases in the same manner, producing the same error values. What are its flaws?
Symmetry is the big one. In its most simple form, the NNE normalization is asymmetric: Black's equity will not always be the additive inverse of White's. Let's examine how EMG preserves symmetry while NNE does not by considering Case A from way back in the introduction: Black trails 3-away, 2-away, with a centered cube.
To calculate Black's EMG, we anchor on the MWC values where Black wins and loses a single game. If he wins he is tied at 2-away for 50%, and if he loses he trails 3-away, 1-away for 24.923%. Now instead, lets look at things from White's perspective. If she wins a single game she leads 1-away 3-away for 75.077%, and if she loses she is tied at 3-away for 50%. Of course, White leading at 1-away 3-away is just another way of describing Black trailing at 3-away, 1-away. Because their EMG lines are always based on the same two points, their EMG values are always the positive/negative reflection of each other and sum to 0. If Black's EMG value is -1.304, White's is +1.304.
Interestingly, this is not the case with NNE. Black's NNE is anchored on what happens when he wins at the current level (he is tied at 2-away for 50%) and when he loses at the next level (0%). White's NNE is anchored on what happens when she wins at the current level (she leads 1-away 3-away for 75.077%, which we plot from Black's perspective at 24.923%), and when she loses at the higher level (0% because Black will give an automatic redouble, which we plot from Black's perspective at 100%). These lines are not the same. They are graphed below, along with the EMG line. Note that the EMG line intersects NNE (Black) at the equity of +1, and intersects NNE (White) at the equity of -1.
Is asymmetry so undesirable? It isn't pretty when Black's equity is 2 and White's -1, but is it important? It means that the reported equity of a position will ping-pong up and down, back and forth, depending upon who is on roll. However, most people look at equity differences rather than absolute values ("I can't believe I made a .06 error!"). Perhaps NNE could be described as evaluating equity differences, and not absolute equity values? A related issue is that a backgammon match is a zero-sum game, so any MWC% given up by one player are acquired by the other. When players are rated on equity lines with different slopes, then one player's errors will be judged out of proportion with the other's. In the diagram above, should Black and White each commit checker play errors giving up 2% MWC, Black's errors will be judged worse because his NNE line is steeper.
There are some steps to try to ensure (or manufacture) symmetry such that both players are rated by the same NNE line. The first is to assume that when the cube has been turned, we should evaluate both players by the cube-owner's NNE line. This makes some sense as only the cube-owner can cash the game at the current level.
When the cube is in the center, why not try to construct a compromise NNE line that both players can use? Perhaps it could follow Black's NNE line when Black is close to a double, and follow White's when she is? We show a Mixed NNE line below that does just that: outside of each player's cash point it follows that player's NNE line. Between the cash points it follows a weighted average of the two lines (which turns out to be the EMG line).
Here, Black's bad pass at 19.822% yields the same error value as it does in Cases B and C on page 2 because it falls on the mixed line where it follows White's NNE line. However, it does not produce the same answer for all three cases when Black makes a good take at, for example, 35%. There, the mixed NNE line diverges from White's.
Finally, let us examine the case where the cube is owned a little more closely. White is tied at 4-away and owns a 2-cube. Since White owns the cube, we need only consider her NNE line. She can cash and reach 2-away 4-away, giving Black 32.8% MWC (graphed at -1), or she lose at the higher level giving Black 100% MWC (graphed at 2). The line differs from the EMG line in that it is not anchored at the "irrelevant" point where Black cashes his 2-cube (which can't really happen since White owns the cube).
5. Conclusions.
Friedman's Normalized Expectation, commonly referred to as Equivalent to Money Game (EMG) has been around for a long time now. It has many valuable properties. (It is only by way of trying to come up with alternatives that one fully appreciates how many valuable properties EMG has.) It is monotonic, linear, symmetric, and perfectly scaled such that a win gives a value of +1 while a loss gives a value of -1. Strangely, it doesn't do the one thing that is currently most asked of it: make comparisons of errors across scores. The very notion of searching through one's match for all errors bigger than .1 or .05 caries the implicit notion that .1 errors are a stable category and are worse than .05 errors. While this may be true on average, there are more exceptions than the current literature acknowledges.
Are these exceptions strange or rare? We have seen how EMG produces inconsistent values across the scores -3 -2, -3 -3, -3 -5; and at the scores -4 -2, -4 -3, -4 -5. These are not strange or rare scores. I would guess that it is the strange and rare match that does not pass through one or more of them.
What do these exceptions mean? We have now examined a case at length in which gnubg's reported errors of .407, .203, and .136 are all equivalent. Suppose we increased the actual error in the third case by a pip, producing an error value of .14. In that case, that .14 error would in fact be worse than the reported .407 error in the first case. If a .14 error can actually be worse than a .407, do EMG error values contain any information at all? One clear answer is that they do—within a match score. These inconsistencies only show up between scores. A .2 error at score X really is twice as bad as a .1 error at score X. But it may not even be worse than a .1 error at score Y. What we do know across scores is that cubes worse than -1.0 are passes. We just can't compare by how much.
In what way does this matter? After all, the bots play well enough, and none of the issues in this paper effect their playing in the slightest. But these issues do effect how they provide feedback to the user, and getting numerical feedback from Snowie and gnubg is how most players advance their game. If we focus on eliminating .1 errors from our game, only to discover that some .05 errors were actually worse all along, we have not been making the best use of our study.
I would like to make the final point that there is no single "correct" normalization. The proper way to evaluate match-play decisions is by way of MWC. Because MWC is sometimes hard to interpret, we use a normalization to make the data more understandable. No normalization is correct; some are simply more useful than others. I hope this paper will spur on exploration for normalizations more useful than EMG.
Acknowledgments
Thanks goes to David Levy for general consultation, and to David Montgomery for much advice and hands-on assistance in mathematical model building.